linerspot.blogg.se

• #Chi square distribution degrees of freedom series

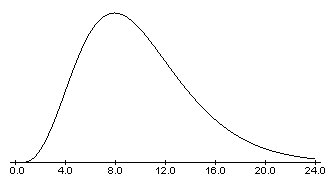
Test statistics based on the chi-square distribution are always greater than or equal to zero. For \(df > 90\), the curve approximates the normal distribution. The chi-square distribution curve is skewed to the right, and its shape depends on the degrees of freedom \(df\). The key characteristics of the chi-square distribution also depend directly on the degrees of freedom. The random variable in the chi-square distribution is the sum of squares of df standard normal variables, which must be independent. These problem categories include primarily (i) whether a data set fits a particular distribution, (ii) whether the distributions of two populations are the same, (iii) whether two events might be independent, and (iv) whether there is a different variability than expected within a population.Īn important parameter in a chi-square distribution is the degrees of freedom \(df\) in a given problem.

#Chi square distribution degrees of freedom series

The chi-square distribution is a useful tool for assessment in a series of problem categories. The mean, \(\mu\), is located just to the right of the peak. Chi-Square Independence Test - What Is It The chi-square independence test evaluates if two categorical variables are related in some population.The mean of the distribution is equal to the number of degrees of freedom. In the R package the pearson.test function in package nortest offers both ($k-m-1$ is the default, but you can get the other bound with a change of a default argument).\). The degree of freedom is one less than the sample size. On the other hand, the distribution function will lie between that of a $\chi^2_$ (where here $m$ doesn't include the total count), so you can at least get bounds on the p-value alternatively you could use simulation to get a p-value. you calculate mean and variance of a supposedly normal sample, then split it into bins for testing for normality) then you don't have a $\chi^2$ distribution at all. If you estimate parameters from ungrouped data (e.g.

However - and this is a pretty big caveat, which quite a few books get wrong - those formulas actually only apply when the parameters are estimated from the grouped data. If you estimate one parameter, you'd subtract 2, and so on. (a) Consider a t distribution with 10 degrees of. The th raw moment for a distribution with degrees of freedom is. x0.22Use the ALEKS calculator to solve the following problems. The chi-squared distribution is implemented in the Wolfram Language as ChiSquareDistribution n. Find the value of 022, Round your answer to three decimal places. The mean of the distribution is equal to the number of degrees of freedom: v. The region under the curve to the right of 0.22 is shaded. This comes up when one thinks about the F-distribution (The 'F' stands for 'Fisher', as in Ronald Aylmer Fisher, one of the most famous 20th-century scientists). If both parameters are specified, you'd only subtract 1. A chi-square distnibution with 13 degrees of freedom is grephed below. Dividing the degrees of freedom by the chi-square random variable results in a distribution of quite a different shape, not merely a rescaled chi-square distribution. So for example, if you estimate both parameters of the normal, you'd normally subtract 3 d.f. Just count how many parameters you estimate, then add 1 when you use the total count. So all you need to do now is figure out how many parameters you estimate in each case and then include the 1 in the appropriate place for whichever formula you use (and that number of parameters is NOT always the same even if you test for the same distribution testing a Poisson(10) is not the same as testing a Poisson with unspecified $\lambda$). Which is to say, when you look properly, everyone agrees, since their definitions of $m$ differ by 1 in just the right way that they both give the same result.

The ones that specify $k-m-1$ define $m$ in a way that doesn't include the total count. Now if you look at their examples, the total count is included in $m$ quite explicitly (there's an example on the very same page they define their $m$ on). The difference from what you said that they say is critical, since the total count is something you calculate from the data. Density Function for Chi-Squared with 4 DF The mean of this distribution is unable to be determined with the information given. Here is the density function for this distribution. A chi-squared distribution constructed by squaring a single standard normal distribution is said to have 1 degree of freedom. Chi Square distributions are positively skewed, as the degrees of freedom increase, the Chi.

Miller and Freund actually specify that their $m$ is "the number of quantities obtained from the observed data that are needed to calculate the expected frequencies" (8th ed, p296). Consider the chi-squared distribution with 4 degrees of freedom. The mean of a Chi Square distribution is its degrees of freedom.